分类
商品
- 商品
- 店铺
- 资讯
线性的概念:
"线性"="齐次性"+"可加性",
"齐次性"是指相似于: f(ax)=af(x),
"可加性"是指相似于: f(x+y)=f(x)+f(y),
而对于单层感知器来说,是无法解决非线性的问题。非线性及不符合上述的条件的集合。
例如异或者问题:
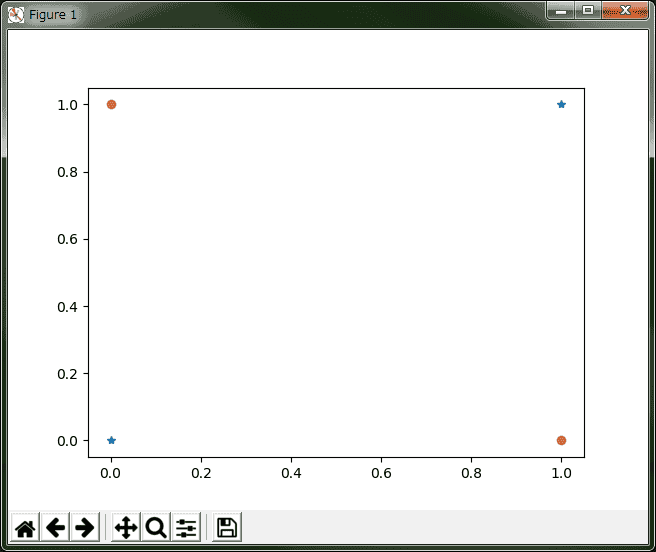 image.png
image.png无法找到一个合适的直线,将两边分离开来。
所以这时候就需要用到了delta法则。
delta 法则的关键思想是使用梯度下降(gradient descent)来搜索可能权向量的假设空间, 以找到最佳拟合训练样例的权向量。
因为在真实情况下,并不能保证训练集是线性可分的。因此,当训练集线性不可分时该如何训练感知器呢?这时我们使用delta法则,通过这种方式可以找出收敛到目标的最佳近似值。
其原理是:
 image.png
image.png由于其激活函数是线性的,所以一般被称为线性单元。
激活函数:
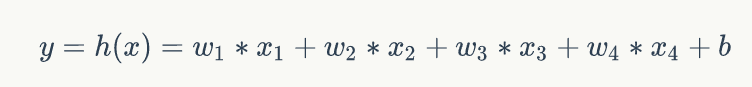 image.png
image.png用向量表示就是:
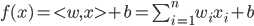 image.png
image.png当然在这一种情况下,还需要考虑其每次计算后的结果的误差,根据误差来调整权值。
而这就需要用到代价函数:
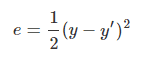 image.png
image.png其中y为期望输出,y`为实际输出。
在求得误差结果最小的情况下,就是我们所求的最优解。注:这里的1/2只是为了后面的计算方便,没有实际意义。
为了求得代价函数最小,由于:
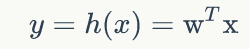 image.png
image.png对路所有的样本的误差和来说:
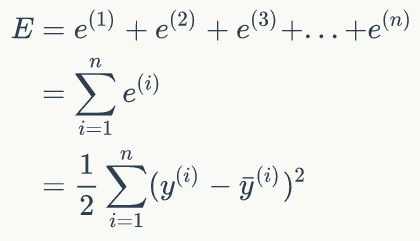 image.png
image.png所以公式可以改写为:
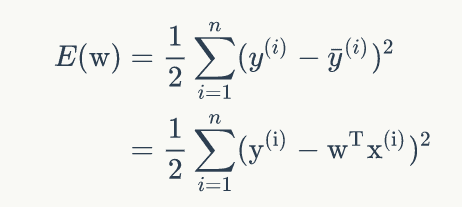 image.png
image.png由于对于样原本说(其实是监督学习的方式),x和y都是已知的,所以上述的公式中其实就是w和E(w)的关系。对整个代价函数来说,其实只有一个变量w。
这样假如想要获取E(w)的最小值,及误差最小,只要要获取的上述变量的最小值就可。因而我们可以使用导数的方式来求取最小值。当然计算机是不会解方程的,所以只能是一步一步的尝试出最小值。
因而引进梯度下降算法:
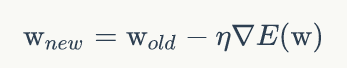 image.png
image.png通过不断的改变w的值,来找到使得E(w)最小的位置:
 image.png
image.png对w求导结果:
 image.png
image.png这样就获取的权值调整公式。
我们可以来看一下推断出来的公式和上一章的单层感知器的差异:
 image.png
image.png其实只有激活函数不一样!!!
下面举个简单的例子说明一下:
输入一组工作年限 [[5], [3], [8], [1.4], [10.1]];
期望输出其代表的年薪:[5500, 2300, 7600, 1800, 11400]
通过随便输入一个工作年限来预算其的年薪。
# coding=utf-8# numpy 支持高级大量的维度数组与矩阵运算import numpy as np# Matplotlib 是一个 Python 的 2D绘图库import matplotlib.pyplot as plt#定义坐标,设定5组输入数据,每组为(x0,x1,)X=np.array([[1,5], [1,3], [1,8], [1,1.4], [1,10.1]]);#设定输入向量的期待输出值Y=np.array([5500,2300,7600,1800,11400]);#设定权值向量(w0,w1)W = np.array([0,0]); #设定学习率lr = 0.01;#计算迭代次数n=0;#神经网络输出O=0;def updateW(): global X,Y,W,lr,n; n+=1; O=np.dot(X,W.T); #计算权值 W_Tmp = lr*((Y-O.T).dot(X))/int(X.shape[0]); #升级权值向量 W = W+W_Tmp;def draw(): global W; x1=[5,3,8,1.4,10.1]; y1=[5500,2300,7600,1800,11400]; #绘制分割线需要的等差数列 x=np.linspace(0,12); #创立子图 plt.figure(); #根据坐标绘图 激活函数:y=x1W1+w0 plt.plot(x,x*W[1]+W[0],'r'); plt.plot(x1,y1,'*'); plt.show();if __name__ == '__main__': #设置迭代次数 for index in range (100): updateW(); #获取组合器输出结果 O=np.dot(X,W.T); #打印 实际值 print O; draw();执行结果:
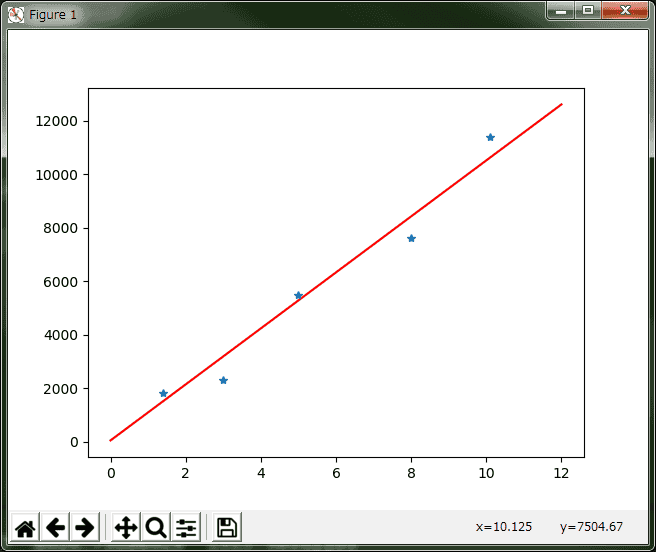 image.png
image.png参考:
线性学习器
https://blog.csdn.net/wasd6081058/article/details/7886697
零基础入门深度学习(2) - 线性单元和梯度下降(写的非常浅显易懂!!!感谢作者)
https://www.zybuluo.com/hanbingtao/note/448086
网易视频课程——深度学习入门系列
http://study.163.com/course/courseMain.htm?courseId=1004111045
 ¥10.80
¥10.80
【老师推荐】同步作文三年级上册四年级上册五年级上六年级下册人教版语文阅读理解专项训练题优秀满分作文范文大全写作技巧书荣恒
 ¥4.30
¥4.30
宝塔钻头大全高硬度钨钢打孔不锈钢专用扩孔开孔器金属扩孔钻阶梯
 ¥16.80
¥16.80
初中生字帖优美句子积累好词好句语文初一高中学生练字帖正楷书钢笔练习临摹本大全硬笔书法小升初七年级八九年级作文专用每日一练
 ¥29.40
¥29.40
宝宝辅食跟我做书 宝宝辅食书婴儿宝宝辅食书婴幼儿辅食大全宝宝辅食大全书婴儿辅食书6个月以上宝宝辅食书宝宝辅食大全书婴儿食谱
 ¥9.90
¥9.90
pe加固线组钓鱼线套装全套正品绑好成品台钓进口主线渔具用品大全
 ¥12.90
¥12.90
中性笔刷题蓝笔红笔黑笔蓝色笔芯按动专用小学生用按压式三色圆珠水笔小白笔速干文具用品大全笔类套装st笔头